Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 [ 93 ] 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

рис. 6.13. зависимость AP/Q-fiQ) для случая осесимметричного течения

а. Расчет /стр.пл

Зная параметр а, можно рассчитать проницаемость, не учитывая при этом величину скин-эффекта zs:

р-" 6.28/1

б. Расчет фтр = /(л)

(6.62)

Если плотность распределения (густота) трещин известна (лг.тр = =lr.Tp), то пустотность фтр может быть выражена как функция коэффициента продуктивности р/=1/л на основании уравнения (6.59) и уравнений, приводимых для различных упрощенных моделей в пятой графе табл. 6.1. Ниже приводится корреляционная зависимость:

тр~ у г.тр-

(6.63)

Для моделей, представленных на рис. 6.6, значения lr.Tp и лг.тр приводятся в табл. 6.2.

таблица 6.2

в. Расчет коэффициента турбулентности р

Коэффициент турбулентности находят непосредственно из уравнения (6.40). Если уравнения (6.42), (6.43) и (6.44) справедливы, то, определив значение параметра В из рис. 6.13, можно проверить

правильность полученной величины /стр.пл-

г. Расчет раскрытости трещины b

Для выбранной модели схематизации раскрытость трещины может быть оценена по табл. 6.1 (графа 7).

6.2.3. Практическое применение моделирования

6.2.3.1. Моделирование отдельной трещины (модель Бейкера)

а. Методика экспериментов

Цель экспериментов Бейкера заключалась в нахождении зависимости Q от ДР для случая радиального симметричного течения в отдельной трещине. Модель, которую он использовал (рис. 6.14), представляет собой монолитный бетонный блок диаметром 3 м, который можно поднимать на разную высоту относительно дна бетонного бассейна и тем самым изменять раскрытость трещины. Центральная скважина радиусом /скв=0,075 м подсоединялась к центробежному насосу, обеспечивая приток (через одну трещину) воды из бассейна, в котором уровень воды в процессе исследования поддерживался постоянным. Исследуемые дебиты изменялись от 160 до 3520 м/сут при изменении раскрытости трещины от 0,125 до 1,0 см. Результаты замеров перепадов давления и дебитов жидкости прн установившемся теченин представлены на графике рис. 6.15.

Ацалнтические зависимости, полученные Бейкером, можно выразить в виде

л н 1 /

=--- п гдр/гд.в".

Рн д1

4 Гскв

1 .66 Гскв

(6.64) (6.65)

Ь 2гскв j

Эти выражения аналогичны выражениям (6.59) и (6.60).

Бейкер установил также зависимость между проницаемостью К в мкм, соответствующей проницаемости пласта с межзерновой пустотностью, раскрытостью трещины 6 в см и толщиной /i в м продуктивного пласта:

/1 = 83,6-10= - .

рис. 6.14. схема эксперимента на модели бейкера.

/ - бетонный блок; 2-насос; 3 - вода; радиусы; гдр - внешнего цилиндра (зоны дреинровання), скв - скважины; b - раскрытость трещины

29 1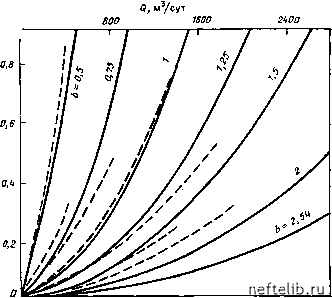

рис. 6.15. зависимость q-др для различных значений раскрытости трещин, полученная в результате эксперимента на модели бейкера. b - раскрытость трещин, мм

При Ь = 0,01 см, /(=0,1 мкм2 эквивалентная толщина продуктивного пласта составляет 0,84 м (если используются результаты экспериментов на модели Бейкера),

б. Результаты экспериментов Бейкера

Из результатов, полученных в экспериментах на модели Бейкера (рис. 6.15), следует, что зависимость Q от АР будет линейной при малых дебитах и нелинейной при значительных дебитах. Линейная зависимость, как и предполагалось, сохраняется даже при высоких значениях Q, если раскрытость трещины достаточно велика. Экспериментами Бейкера была подтверждена возможность использования уравнений, описывающих процесс течения в пористой среде, для этого же процесса в трещиноватых пластах.

в. Сопоставление результатов эксперимента с аналитическими оценками

В качестве экспериментальных данных использованы дебиты и перепады давления, наблюдаемые (из экспериментов Бейкера) при раскрытости трещины Ь==1 см (рис. 6.15).

1. Замеренные значения Q в зависимости от ДР (см. рис. 6.15) преобразуются в зависимость AP/Q от Q, как показано на рис. 6.16.