Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 [ 169 ] 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

дования глубинных проб нефтей показывают, что давление насыщения в них значительно снижено. Это подтверждает то, что конвективный перенос имеет место в нефтенасыщенной зоне.

Конвективный перенос в трещине, обеспечивающий обменные процессы между трещиной и матрицей, также был рассмотрен Пис-меном [5] на примере вертикальной трещины с шириной раскрытия Ь, проницаемость которой составляла /Стр = Ь/12.

а. Основные уравнения

Уравнение материального баланса газа, растворенного в нефти, находящейся в трещине, должно учитывать явления диффузии, конвекции, переноса из матрицы в трещину и аккумуляции:

г.н-тр г.н-тр

=~дх ду

+ ..rp = -f- (10.25)

Уравнение материального баланса растворенного газа в матрице

Vrp dt

9м-хр = -- (10.26)

где Vm/Vtp - объем нефти в матрице на единицу объема трещины. Было принято, что плотность нефти линейно зависит от Яг.н.

откуда с учетом уравнений (10.25) и (10.26) получим

[ дх- df 1 дх ду ~ dt

Vtp dt

(10.27)

-5 = м(Р.р-Р«). (10.28)

Ктр ot

где /См - коэффициент переноса, б. Метод возмуиений

Если обмен между матрицей и трещиной отсутствует (/См==0), в трещине высотой Я и шириной b (считая ее конвекционной ячейкой) возмущение может быть результатом обратного градиента плотности. Возмущение будет нарастать экспоненциально как е", где ю выражает фактор роста возмущения (рис. 10.27).

Рис. 10.27. Профили плотностей при синусоидальном возмущении за счет обратного градиента плотности [5]

Фактор со зависит от физических параметров и должен быть одинаковым как в матрице, так и в трещинах. Таким образом, выражение, описывающее развитие возмущения, имеет следующий вид:

0) +

/m+Im/ItpJ

£2 = mu/o),

(i.DTp

(10.29)

(10.30) (10.31)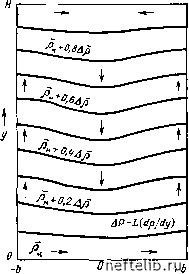

(10.32)

Уравнение (10.29) показывает, что массоперенос определяется параметрами Кш и Vm/Vtp, т. е. фактор роста возмущения может быть переопределен для случая отсутствия обмена между матрицей и трещиной следующим образом:

0)„ = О) +

(10.33)

Устойчивость и неустойчивость системы с инверсным распределением плотностей по высоте может быть оценена из уравнения (10.29).

Неустойчивость состояния системы соответствует положительным значениям ю, поскольку возмущение будет экспоненциально расти, а при отрицательных значениях ю система останется устойчивой, что будет соответствовать стабильной инверсии плотности.

Итак, из уравнения (10.29) следует, что устойчивость или неустойчивость системы с инверсной плотностью зависит от величины ю: при (й>0 система неустойчива - возмущение возрастает экспоненциально; при (й<0 система устойчива - возмущение затухает; при ю = 0 система находится в метастабильном состоянии.

в. Общие замечания

Результаты изменения различных факторов следующие: для

/См/Сйн>10 (й/Юн=1-/См/сОн; для Лм/Сйн<0,5 Сй/(йн= 1/(1-I-Ум/Утр).

тз оЬычных случаях приведенные параметры характеризуются следующими порядками величин: /См>10-с-; 50< 1/м/Утр<100; ю/юн - единицы процентов.

Неустойчивость инверсии плотности не зависит от наличия или отсутствия переноса между матрицей и трещиной. Для трещины высотой 300 м горизонтальная протяженность зоны возмущения составляет приблизительно 10 м. Градиент инверсной плотности растет экспоненциально е Для трещин большой протяженности фактор роста возмущения ю целиком и полностью зависит от Dp.

10.3.5. Механизм нефтеотдачи в зоне заводнения

Механизм нефтеотдачи единичного блока матрицы в зоне заводнения, связанной с гравитационными силами и капиллярной пропиткой, детально обсуждался в гл. 9. Если серия вертикальных блоков разделена горизонтальными трещинами, то процесс вытеснения нефти происходит вследствие перемещения ВНК в трещинах. Причем начинается капиллярная пропитка единичных блоков.

Методы моделирования и их физические особенности практически ограничиваются критериями, обсуждавшимися в гл. 9, где показано, что перенос результатов моделирования на месторождение в целом может быть осуществлен разными путями.

10.3.5.1. Экспериментальный подход - метод Маттакса

Характеристики капиллярной пропитки блоков матрицы можно определить при помощи лабораторных экспериментов, в которых учитываются безразмерные критерии подобия:

(10.34)

. пл-бл

Таким же путем результаты лабораторных экспериментов, выполняемых на кернах, можно использовать для изучения зависимости нефтеотдачи от времени для серии вертикально расположенных блоков матрицы.

Для решения указанной задачи необходимы основные исходные данные: свойства жидкостей; характеристики блоков - К, Ф, в.нач, Ябл; характеристики залежи - высота залежи Hi, ее площадь А; скорость перемещения ВНК в трещинах Ивнк; в зависимость нефтеотдачи от времени, полученная на основе экспериментальных исследований (рис. 10.28).

Расчеты сводятся к следующему.

Преобразуем зависимость нефтеотдачи от времени, определенную в результате лабораторных экспериментов (см. рис. 10.28) на кернах, в такую же зависимость для залежи в целом при помощи уравнения (10.34), т. е. найдем для зависимости на рис. 10.28 новый масштаб времени: