Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 [ 5 ] 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

ч-Рис. 1.20. Изменение с глубиной пластичности водонасыщениых пород [10]. / - нзвестнякн; 2 - песчаники; 3 - доломиты; 4 - кварциты

Рис. 1.21. Изменение среднего числа трещин в зависимости от литологии пород [10]. / - кварциты; 2 - доломиты; 3 - кварцевые пес-

. чаннкн; 4-песчаники с кальцнтовым цементом;

1 5 - нзвестнякн

о 10 го jd

пластичность, % остаточной деформации, перед образованием разлома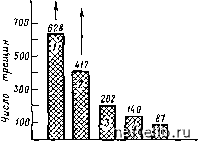

литологические типы пород

НИЯ В них И увеличение их пластичности. по-видимому, карбонатные породы более чувствительны к влиянию температуры, чем кремнистые. влияние температуры на известняки показано на рис. 1.19.

в. Тип породы

механические свойства осадочных пород также были детально изучены хандином [10], и все же, по-видимому, преждевременно говорить о надежности установленных зависимостей для различных материалов, слагающих породы [1].

можно утверждать, что в общем случае увеличение пластичности материала обусловливается увеличением давления сжатия и температуры при уменьшении скорости деформации. при одних и тех же условиях кварциты и доломиты никогда не становятся такими пластичными, как известняки. степень сцементированности песчаников следует считать средней между известняками и доломитами. на рис. 1.20 показано изменение пластичности пород с глубиной захоронения, выражаемой через средние градиенты температуры и давления (за счет нагрузки вышележащих пород). на небольших глубинах различия в пластичности пород оказываются незначительными, но на глубине нескольких тысяч метров они становятся существенными.

различие в пластичности могло сильно повлиять на количество трещин, образованных в различных породах при одной и той же глубине захоронения (рис. 1.20). и действительно, результаты, полученные в лаборатории, показывают существенно неодинаковое количество трещин для горных пород разных типов, залегающих в сходных условиях (рис. 1.21).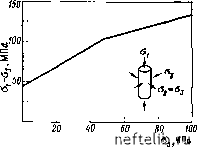

рис. 1.22. прочностные характеристики известняка при долговременном нагру-жении

г. Прочность пород

Так как оценку свойств горных пород, обусловленных воздействием среды в течение длительного времени, по данным кратковременных лабораторных испытаний при трехосном сжатии вряд

ли можно считать надежной, было предложено использовать для этой цели предел упругости. Иначе говоря, использовать тот факт, что на кривой напряжение- деформация имеется такое предельное значение напряжения, при превышении которого линейная зависимость между нагрузкой и деформацией нарушается. Это предельное значение, которое называется «началом нелинейности» на кривой напряжение - деформация, соответствует началу процесса образования трещин, так как к этому моменту в образце породы появляются многочисленные микротрещины.

Кривую для оценки начала трещинообразования в породе, залегающей в условиях данного пласта, можно получить путем построения зависимости дифференциального напряжения а\-аз от бокового сжатия аз (рис. 1.22). При напряжениях, соответствующих существенному изменению наклона этой кривой, начнется растрескивание породы. Упрощенно кривую можно представить в виде двух отрезков ломаной линии, причем изменение ее наклона будет соответствовать хрупко-пластичной переходной зоне. Использование этого метода позволяет установить критерий образования трещин для всех главных напряжений в условиях сжатия или растяжения.

1.3. геологическая модель трещинообразования

Модели процесса трещинообразования были недавно предложены Киблье [И] и Рамстадом [8 . Главной целью модели, предложенной Киблье, было нахождение областей наибольшей густоты трещин или наибольшей вероятности трещинообразования путем расчета ряда карт равной вероятности развития трещин. Его основная идея заключается в том, что тектонические напряжения в пласте можно рассчитать, используя современную (известную) форму различных слоев и полагая, что первоначально они были плоскими. Суммарные напряжения складываются из тектонических напряжений и нагрузки вышележащих пород (горного давления). По этим суммарным напряжениям и критерию (условию) разрушения определяются густота и распределение трещин.

С помощью такого метода был рассчитан критический модуль упругости в каждой точке и оценена достаточность его величины

для начала трещинообразования при данном смещении пород. В точках с наименьшим критическим модулем вероятность трещинообразования при данном смещении пород будет выше и наоборот. Эта модель использовалась при анализе месторождений Ирана.

Модель Рамстада сохраняет основную идею Киблье -задание известных смещений пород, но метод моделирования в этом случае другой. Рамстад использовал метод конечных элементов в условиях закона линейности для упругих и упруго-вязко-пластичных материалов.

1.3.1. Моделирование, основанное на методе конечных элементов

Этот метод основан на разделении всей области залежи на отдельные подобласти (элементы) и представлении в пределах каждой подобласти интересующих нас полей в виде многочленов. Непрерывность на границах между элементами также выражается определенными условиями, накладываемыми на функции поля.

Данный метод имеет несомненные преимущества в условиях сложной геометрии неоднородных пород. Его также можно использовать при решении задач в случае вязко-пластичного материала. Под элементом в данной работе подразумевается четырехсторонний плоскодеформируемый элемент, имеющий две степени свободы в каждом углу или узловой точке (рис. 1.23). Матрица жесткости получается использованием 2X2 гауссовского интегрирования, в то время как напряжение в случае анализа вязко-пластичного материала вычисляется в четырех точках гауссовского интегрирования, а в случае анализа линейно-упругого материала - в центре элемента [8].

1.3.2. Формулировка конечного элемента в случае вязко-пластичных пород

При разделении структуры на конечные элементы поле смещения пород (U) внутри каждого элемента выражается посредством значений в узловых точках (V) и интерполяционными функциями. Основные уравнения этой дискретной системы дифференциальных уравнений следующего вида:

1. Связь между приращениями

Рис. 1.23. Четырехсторонний плоский элемент