Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 [ 99 ] 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

Ъодл<

log Re

Рис. 6.25. Кривая зависимости log Я,-log Re при течении газа через пористую среду и трещины с малой раскрытостью (0,0115-0,45 мм). Условные обозначения см. ва рис. 6.24

чалось путем деления расхода р,, замеренного на входе в трещину, на ее сечение:

q = qJbYWM.

Градиент давления выражается в виде APIL={P\-P2)/L, т. е. как разница давлений в точках входа в единичную трещину и выхода из нее, отнесенная к длине трещины.

На рис. 6.24 прямые линии с углом наклона 45° в логарифмическом масштабе (log-log) характеризуют линейную зависимость между q и градиентом давления dPjdx при ламинарном течении. Ограничены эти отрезки прямых линией А-А\ Для этого интервала перепад давления или расход рассчитывается по уравнениям (6.75) и (6.75) (см. табл. 6.4).

При расходах 200-300 см/сут и при больших значениях раскрытости трещины b переходная зона отмечается даже при малых градиентах. Как видно на рис. 6.24, за пределами переходной зоны градиент давления значительно возрастает при малых приращениях расхода. Линия В-В соответствует линии критическогодав-

ления, которое связано с максимальной скоростью на выходе из трещины.

На рис. 6.25 представлена зависимость x от Re, основанная на уравнениях (6.77) и (6.78) (см. табл. 6.4). Интересно отметить,что при ламинарном течении газа сохраняется та же основная зависимость, которая была получена для течения жидкости в трещинах:

X = б/Re.

Из этого следует, что критическое число Рейнольдса для случая течения газа может быть принято равным примерно 1000 (см. рис. 6.25).

Эксперименты показали также, что при турбулентном течении газа через трещину (Re>1000) зависимость Блазиуса к-Re может быть выражена в виде

X = 0,056/ Re°•2

где X и Re определяются по уравнениям (6.77) и (6.78) (см. табл. 6.4).

6.3.2. Радиальное осесимметричное течение газа к скважине

Аналогично тому, как на основании данных экспериментов по исследованию течения газа в единичной трещине, рассмотренных в разделе 6.3.1, сделан вывод о возможности использования закономерностей течения жидкости для случая течения газа, так, очевидно, и решения, описывающие течение в пористой среде, могут быть применены при изучении фильтрации в трещинной системе.

Рассматривая результаты исследования течения газа к скважине в пористой среде и вводя специфические характеристики, отражающие особенности трещиноватого пласта, была разработана методика приближенных расчетов, приведенная ниже.

Основное соотношение между падением давления и скоростью течения газа при турбулентном и ламинарном режимах в общем виде выражается уравнением

AiP) = AQ + BQ\ (6.81)

По аналогии с обычным пластом, характеризующимся межзерновой пустотностью, это уравнение может быть представлено следующим образом:

Д (Р2) = 0,135 (1пГдр/Гекв + 25) +

+ 3,16-10-" iIl/-J---L\ (6.82)

где Q - в м/сут; Р - в ат; /С - в мД; Г - в К; р - в 1/м; г - в м.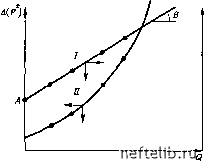

рис. 6.26. кривые основных теоретических зависимостей Q-A(P)JQ {/) и q-д(Р2) ( ) при течении газа через систему трещии

тр.скв,

замеренных при

Методика расчета аналогична методике оценки параметров потока при движении газа к скважине в пласте с межзерновой пустотностью. На основании данных о Q, установившемся режиме, урав-

нение течения A(P)/Q = /(Q) представляется в виде А (P)/Q = A + BQ.

(6.83)

Представив завнсимость A{P)/Q от Q отрезком прямой, как показано на рис. 6.26, можно рассчитать: значение А при Q = 0;

значение В - по наклону прямой, выражаемому A[A{PIQ]/AQ.

/Стр.пл можно рассчитать по уравнению (Лтр.пл - в мД)

Л = 0,135

.тр.пл

1п др/cKB

-1-25

(6.84)

где А и все параметры известны, в том числе величина SS, которая получается в результате интерпретации замеров давления при неустановившемся режиме фильтрации.

Коэффициент турбулентности р можно определить косвенно через параметр В из уравнения

5=3,16-10-19 щ1.

(6.85)

илн по уравнениям (6.42), (6.43) и/или (6.44).

Необходимо сделать следующие замечания.

Рассмотренный прием представляет собой простое распространение методов, разработанных для газоносного пласта с межзерновой пористостью, на трещиноватый пласт, и поэтому пользоваться им можно только в случае, если густота трещин высокая и распределение трещин относительно равномерное.

В случае скважины с открытым забоем для расчета В обычно используется уравнение (6.85), включающее величину общей продуктивной толщины h, тогда как в случае частично открытого забоя или частично перфорированной скважины в это уравнение необходимо вводить скорректированное значение толщины йэф. Эта корректировка имеет существенное значение, поскольку параметр В должен так или иначе учитывать влияние геометрического скип-эффекта.