Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 [ 55 ] 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

Экспериментальные результаты анализа керна нанесены на полулогарифмический график (рис. 4.21) и получена прямая линия (уравнение (4.44)).

Чтобы проверить надежность полученной зависимости, выраженной прямой линией, используют средние величины проницаемости и пористости, найденные по гистограммам (рис. 4.22, а, б): среднее значение Фм, равное 29,5%, соответствует среднему значению Дм 0,0012 мкм2.

При отсутствии данных анализа керна можно использовать различные эмпирические зависимости, приведенные в литературе. Графики на рис. 4.23 показывают зависимость Фм-Дм для различных типов пород. Имеются многочисленные аналитические выражения зависимости Фм-Дм, среди которых выделяется формула Требина [8] для различных значений пористости:

-0,316Ф

при Ф„<12% Дм = 2е ;

при Фм> 12 % Дм = 4,94 Ф - 7,63.

В общем уравнение для низких значений пористости дает величины, близкие установленным по керну, и, если сравнить график этого уравнения с графиками на рис. 4.23, можно отметить хорошее совпадение его с графиком для рифовых известняков.

а. Статистический метод [15]

Приведенное выше уравнение (4.19) обладает интересной особенностью при выполнении условия, что данная пористость Фм соответствует данной проницаемости Дм при всех значениях

x* = (4.46)

согласно уравнению

logДм = (Фм-Ф) -+ logД = aФм + 6, (4.47)

где Ф - среднее арифметическое значение пористости;

»Ф = ФстанД.откл-Ф> (4-48)

Фстанд. откл - пористость при данном стандартном отклонении от Фм;

ах =logДcтaнд.oткл-logД, (4.49)

Дставд. откл - проницаемость при данном стандартном отклонении от Км,

а=-102(1-У)/Ф„Уф ; (4.50)

b = - аФ\ogK ; (4.51)

о я я я ч Е о 3

" й 2

J- w

.J м ч

>3й

s я 3 g

S я о о

о s л

о о " u П S ro о

я о м а ova

3 = 5 я

К О OsM

О ь

я о )а

m н m

г-а to

W 2 о о

U S Ш о

П) ГО К bi

q * )а Я

гттгг

S S

о я S

о t3 S

3 ° Е

о 9 ?

Частость Встречаемости, % ei Частость бстречаемости , % 9

*- ов ?5

-I-г-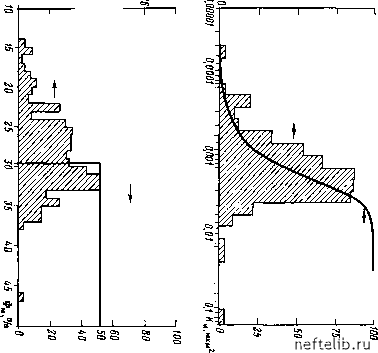

Накопленная частость, %

Накопленная частость,%

v.= "-- (4.52)

v, = . (4.53)

Основываясь на статистической оценке данных о Фм и Км при их нормальном и логнормальном распределении и определив значения 0к, Оф, /С и Ф можно решить уравнение (4.45) [15]. Пример [15]. Известны следующие данные:

Ф = 0,2 - среднее по интерпретации результатов ГИС; Ф84.1 = 0,13- со стандартного вероятностного графика данных, пористости при стандартном отклонении 84,1%; К=100 мД (0,1 мкм) -среднее геометрическое по интерпретации диаграмм, полученных при испытании пласта пластоиспытателем на буровых трубах; Vk = 0,7 - вариация проницаемости по Дикстре - Парсону, полученная по аналогии.

Тогда зависимость К от Ф будет выведена следующим образом.

По уравнению (4.53)

Д84,1==(1-)Д-(1-0,7) 100 мД = 30 мД; по уравнениям (4.48) и (4.49)

Оф =фз,, ф = 0,13 -0,2 = 0,07;

Ох = log а:84.1 - log К\ = log 30 - log 100 = 0,523; далее по уравнениям (4.52) и (4.53)

= 1 = : = 0,35; ф 0,2

= = 0,7,

к 100

откуда

log(l-vx) °g(-0.7) ~ ф 0,2X0,35

Ь = -аФ + logj = - (7,47) (0,2) + log 100 = 0,506.

Зависимость Км от Фм, в соответствии с уравнением (4.47) принимает вид

logДм=(Фм-0,2 )-MoglOO

или

log а:„ = 7,47 Ф-Ь 0,506.