Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 [ 143 ] 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

Время

Рис. 9.33. Зависимость нефте- Рис. 9.34. Зависимость относительной нефтеотдачи от времени отдачи от безразмерного времени

Скорость капиллярной пропитки, учитывая структуру модели Аронофски, Де-Сваан [16] предложил записать в следующем виде:

(9.57)

В дальнейшем можно принять, что расход впитываемой воды на единицу длины трещины составит

£кон О

(9.58)

Замечания. Зависимость InjR от времени t, описываемая выражением (9.55), не подтвердилась в экспериментах Иффли (рис. 9.35). Однако отклонения от прямой линии в полулогарифмических координатах получились наименьшими для блоков небольшой высоты и малой проницаемости (сравните обр. С с обр. В на рис. 9.35).

Конечный коэффициент вытеснения (63%) был получен Мат-таксом в экспериментах на алундовом образце, когда начальная водонасыщенность образца составляла 5в.нач=0, что совпадает с выражением (9.60), когда t->-к.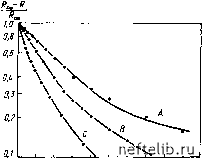

Рис. 9.35. Зависимость относительной нефтеотдачи от безразмерного времени в экспериментах Р. Иффли [11]:

w 20 30 W 50 во 10 80 90 А

о s ю 15 га 25 30 35 в о 50 100 150 200 250 300 350 ш с

Аналогичный результат может быть получен путем решения уравнения (9.60), если отношение подвижностей М = 1 (уравнение 9. 23), так как в этом случае Zc = Z эквивалентно нефтеотдаче. Физическое время /б.гр, как полагает Дю-Прей [9], соответствует времени перемещения фронтовой насыщенности на высоту

Я = О.бЗЯ (9.59)

в случае, когда вытеснение происходит только за счет гравитационных сил из полностью погруженного блока, причем отношение подвижностей Мл1.

б. Уравнение Боксермана [5]

Выражение, полученное Боксерманом, может трактоваться как аналитическое упрощение выражения (9.19), основной модели, описанной в разделе 9.2.

Решение этого уравнения показывает, что при очень малых значениях М

2б» const/б.и. (9.60)

что эквивалентно

R const ]/" /б • (9-60)

Это уравнение хуже коррелируется с результатами экспериментов Иффли [11], чем с результатами опытов Маттакса.

в. Модели Кайта и Маттакса [7]

Эксперименты этих исследователей проводились на двух типах образцов:

Алундовые образцы Образцы песчаника

Форма......... Полу цилиндрическая Кубическая

Герметизация ,..... Боковых поверхностей Отсутствует

Водонасыщеиность . . . Sg „д, =0 Sga,. =0

Экспериментальная схема Рис. 9.36, а Рис. 9.36, б

Результаты, полученные при противоточной пропитке алундо-вых образцов, приведены на рис. 9.37. За одно и то же время большая нефтеотдача получена при наименьшей вязкости воды из образцов большей длины и для пород, характеризующихся более высокой проницаемостью.

Опыты по трехмерной пропитке проводились при различных, но постоянных скоростях подъема ВНК в трещинах (подобно случаям 2 и 5 рис. 9.31). При интерпретации результатов экспериментов была выдвинута концепция критической скорости подъема ВНК. Критическая скорость соответствует моменту равной скорости пе-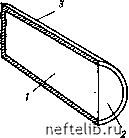

Несрть

Образец

Рис. 9.36. Опыты С. Маттакса [4] по капиллярной пропитке: а - противоточной; б - трехмерной.

/ - образец; 2 - грань, открытая для пропнткн; 3 - непроницаемое пластиковое покрытие; 4 - плексигласовый контейнер; 5 -опоры для установки образца; - подача воды (измеряемый объем); 7 -положение ВНК; S -выход иефти

ремещения ВНК в трещинах (уровень воды) и в матрице (фронт вытеснения). Причем скорость большая, чем критическая, соответствует более быстрому перемещению ВНК в трещинах, чем в матрице (рис. 9.38, б); обратным соотношением характеризуется скорость, меньшая критической (см. рис. 9.38, а). Перемещение ВНК с критической скоростью соответствует одинаковому положению ВНК в матрице и трещинах (см. рис. 9.38, в).

С учетом этой концепции считалось, что величина конечной нефтеотдачи матрицы достигается при скоростях подъема ВНК в трещинах меньших критической (см. рис. 9.38, а) в момент подхода фронта вытеснения к верхней грани матричного блока. Было установлено, что величина нефтеотдачи изменяется в -зависимости от скорости подъема ВНК в трещинах в несколько раз при скоростях, меньших критической. С целью оценки критической скорости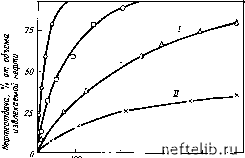

т 300

время, мин

Рис. 9.37. Результаты экспериментов по противоточной -капиллярной пропитке [4]:

Полное время пропитки: / - 1250 мни, II - 9000 мни.