Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 [ 167 ] 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238

Считая, например, заданными динамические забойные давления и определим дебиты взаимодействия скважип:

2iTbk

(Рк - pi) In

2q2 Rc

(Pk -P2) In

(«2 + ai) + 45

(a2 - ai)-

2a: Rc

(«2 + ai) + 45

(a2 - ai) + 45

(33, XX)

27гЬк

(Pk -P2) In

(Pk - pi) In

(«2 + ai)

(a2 - aif + 45

202 Rc

Рис. 169. Две скважины Ai и A2, симметрично расположенные но отношению к контуру области питания.

(«2 + aiY + 45

(34, XX)

(а2 -aif + 45

При ai = «2 = pi = Р25 т. е. когда две рав-нодебитные взаимодействуюгцие скв. Ai и А2 расположены на одинаковом расстоянии а от контура области нитапия (рис. 169), из последних формул получим:

Qi - Q2

jl In

2а Уа + 5 Rc5

(35, XX)

Чтобы определить дебит Qi одиночно работаюгцей скв. Ai с динамическим давлением па забое pi, можно воспользоваться формулой (35, XX), положив в ней оо и pi = pi:

27гЬк{рк - pi)

fi In

(36, XX)

Последняя формула совпадает с ранее выведенной другим способом формулой (41, XIX). В отличие от формулы (26, XX) из формулы (35, XX) получен совергаенно правильный вывод: при любом конечном расстоянии между скважинами в одном и том же однородном

пласте опи будут взаимодействовать друг с другом: Qi Qi лигаь при оо.

Рассмотрим другой случай: две взаимодействуюгцие скв. Ai и А2 радиуса Rc с дебитами Qi и Q2 расположены произвольным образом по отногаепию к круговому контуру области питания Aj (рис. 170).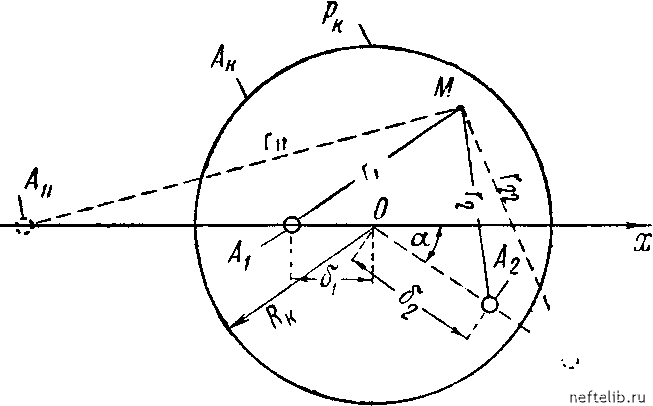

Рис. 170. Две скважины Ai, и А2, расположенные произвольным образом по отношению к круговому контуру области питания Ак-

Поместим в центрах скв. Ai и А2 точечные стоки, производительность которых равна соответственным дебнтам скважин на единицу могцностн пласта. Отобразим в окружности Aj стоки Ai и А2 источниками Ац, А22 (эксплуатационные скважины отображаем на-гнетательными скважинами; их центры - точечные стоки и источники должны быть точками «взаимно сопряженными» по отногаепию окружности Aj; см. § 4 главы XIX). При таком расположенни равноде-битных стоков и источников окружность будет служить изобарой, что и необходимо по условию задачи. С помогцью метода отображения источников-стоков задача о взаимодействии двух скважин внутри кругового контура регаается темп же приемами, что и регаенная перед этим задача с прямолинейным контуром области питания. Из-за громоздкости не будем здесь приводить окончательных формул для изображенного на рис. 170 случая произвольного расположения скважин (см. нодробности в книге Щелкачева и Пыхачева [203]). Ограничимся более простым случаем, изображенным на рис. 171, когда скважины Ai и А2 радиуса Rc расположены симметрично но отногаепию к контуру

области питания А, на котором давление поддерживается равным р. Считая, что динамические давления па забоях скважин р[ и Р2 одинаковы и обозначая расстояние между центрами скважин через 25, дебиты Qi и Q2 определим из формул:

Qi ~ Q2

27гЬк{рк -pi)

/iln--

2RlRc5

(37, XX)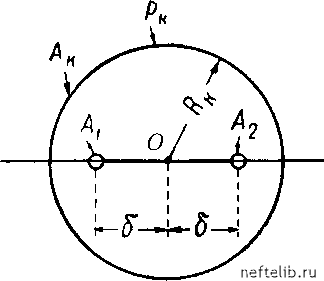

Рис. 171. Две скважины Ai и А2, расположенные симметрично по отношению к центру О кругового контура области питания Ак

Когда величина ла но сравнению с что Rt - 5

5 столь ма-величипой Rk ,

R, из формулы (37, XX) получаем приближенную формулу (26, XX). С другой стороны, точная формула (37, XX) не приводит к таким парадоксальным выводам, к каким приводила приближенная формула (26, XX) нри больгаих расстояниях между скважинами. Действительно, полагая, например, в формуле (37, XX) р[ = Pl, 25 = Rk и сравнивая результат подстановки с формулой (46, XIX) (в которую также надо

подставить d = Rk) для дебита Q

одиночной скважины, видим, что Qi < Q.

Итак, точные формулы (33, XX) и (37, XX) позволяют регаать задачи о взаимодействии скважип, расположенных вблизи контуров области нитапия соответствуюгцей формы, и, кроме того, позволяют оценить степень погрегапости результатов подсчетов по приближенной формуле (26, XX). Сравнительные числовые подсчеты по выведенным выгае формулам будут выполнены в следуюгцих параграфах.

§ 3. Анализ семейств траекторий и изобар и распределения скоростей фильтрации в пласте в случае двух взаимодействующих

скважин

При анализе семейств траекторий и изобар будем сначала базироваться па ириближенпой формуле (6, XX), при выводе которой пе