Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 [ 60 ] 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238

фильтрации вблизи забоя должна неограниченно возрастать (чтобы получить конечный расход потока, необходимо неограниченпо увеличивать его скорость, если плогцадь поперечного сечения потока неогра-пичепно убывает).

Конечно, последние перечисленные выводы либо противоречивы, либо физически нереальны, их абсурдность указывает на то, что приближенные формулы дебита, а также формулы (20, X) и (23, X) можно применять только с известным ограничением. Действительно, приближенные допугцения (о горизонтальности скоростей фильтрации и т. д.), лежагцие в основе вывода всех нриведепных выгае формул, справедливы тем с больгаей точностью, чем меньгае понижение уровня жидкости в скважине и чем мепьгае глубина фильтрационного потока, т. е. чем больгае размеры пласта (радиус К) по сравнению с первоначальной могцпостью /Ik водоносного слоя. Поэтому нельзя пользоваться формулой Дюпюи для анализа максимально возможного понижения уровня жидкости в скважине. Наоборот, нри сравнительно малых понижениях уровня этой формулой с успехом пользуются в гидрогеологической практике.

Учитывая приближенность допугцения Дюпюи, Козепи попытался провести более строгое исследование движения жидкости со свободной поверхностью.

Эти исследования также оказались далеко пе точными, а предложенные расчетные формулы были весьма громоздки. Однако справедливо была отмечена важность явления «скачка» (прыжка). Сугцпость этого явления состоит в следуюгцем: в процессе откачки воды из колодца (скважины) динамический уровень в нем оказывается стоягцим ниже, чем уровень воды в пласте пепосредствепно у степки колодца.

На рис. 65 схематично изображены: динамический уровень АВ воды в колодце M7V, уровень ЕС воды в пласте у стенки колодца, вертикальные сечения CD и ЕЕ ближайгаей к колодцу части свободной поверхности воды в пласте.

Точки Е и С лежат выгае АВ, длины отрезков АЕ и ВС определяют высоту «скачка». Поверхность стенки колодца па участке ЕА называется поверхностью высачивания.

Экспериментальные и теоретические исследования других авторов [120 и др.] показали, что сугцественное влияние на приток воды к скважине оказывает так называемый «капиллярный слой» воды над ее свободной поверхностью в пласте. Чем больгае высота столба воды в скважине и в области питания по сравнению

Глубокие исследования движения воды в пласте в условиях гравитационного режима (при учете граничных условий на поверхности высачивания) были выполнены П. Я. Полубариновой-Кочиной [143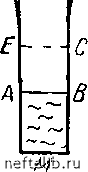

с высотой капиллярного поднятия, тем меньгае влияние капиллярного слоя и тем точнее оказывается формула (21, X). Следует отметить, что егце более чем за 40 лет до появления упомянутой работы американских авторов, в конце 80-х годов прогалого века, проф. Н. Е. Жуковский отмечал необходимость учитывать явления капиллярного поднятия при изучении движения грунтовых вод.

Новейгаие исследования вновь подтвердили высокую точность формулы дебита (21, X) при малых пониженных уровнях жидкости в скважине и, наоборот, выяснили довольно значительные неточности формулы (23, X), служагцей для определения формы свободной поверхности жидкости в пласте.

Перейдем к изучению радиального притока к скважине жидкости со свободной поверхностью в том случае, когда в пласте справедлив нелинейный закон фильтрации.

Сохраним все условия рассматриваемой задачи, сформулированные в начале данного параграфа, но допустим, что движение жидкости во всем пласте подчиняется не линейному закону фильтрации, а нелинейному. Тогда вместо формулы (17, X) получим:

Рис. 65. Схематичное изображение «скачка» при переходе от уровня воды в колодце к уровню воды в пласте.

dz dr

(28, X)

где сип - постоянные величины, причем 1 < по <С 2. Разделим переменные z и г в последнем уравнении:

27ГС

(29, X)

Для определения формы депрессионной кривой проинтегрируем

При сравнении с формулами главы VII и здесь следует учитывать, что п = см. подстрочные примечания к формулам (64, IX) и (14, X)

уравнение (29, X)

откуда

По + 1

/.по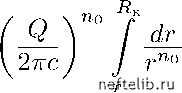

+1 щ + 1 ( Q\

По - 1

у2теу

по-1 по-1

(30, X)

(31, X)

Для вывода формулы дебита скважины проинтегрируем уравнение (29, X) в других пределах: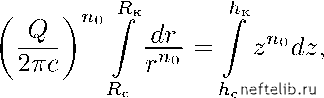

(32, X)

откуда

Q = 27ГС

- 1 К -

По + 1

(33, X)

Конечно, последнюю формулу можно было бы вывести из уравнения (31, X), положив Z = he, г = Rc.

Заметим, что при и при значении щ не слигаком близком

к единице, величиной можно пренебречь по сравнению с i-

Если в формуле (33, X) принять по = 2, то получим формулу, впервые выведенную Краснопольским для трегциноватых пород.

Заметим, что формулы (28, Х)-(33, X) могут иметь лигаь огра-пичепное применение, указывая влияние наругаепия линейного закона фильтрации в том теоретически возможном (или осугцествлепном в эксперименте на специальной модели) случае, когда наругаепие закона фильтрации охватывает весь нласт. Как показывают рассуждения § 6 главы IX, при движении к скважине жидкости со свободной поверхностью было бы нравильпее учитывать возможность появления ограпичепной зоны кризиса линейного закона фильтрации и рассматривать движение жидкости при одновременном сугцествовании по крайней мере двух (а егце правильнее нескольких) режимов фильтрации.