Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 [ 43 ] 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238

Рис. 50. Элемент радиального потока

эадиуса г и высоты 6, равной могцности (высоте) потока (см., например, рис. 44 и 45):

F = 27ГгЬ. (11, VIII)

Если в основной плоскости течения поток ограничен радиусами АО и ОВ, то под F следует подразумевать лигаь часть боковой поверхности цилиндра.

Предположим, что на рис. 50 точка О является центром, к которому сходятся прямолинейные траектории трехмерного радиального потока. В таком случае формулы (9, VIII) и (10, VIII) останутся без изменения, но под F надо подразумевать плогцадь соответствуюгцей части поверхности сферы. Так, например, если считать, что рис. 50 является элементом потока, изображенного на рис. 46, то для всего изображенного на рис. 46 потока F будет равно поверхности полусфе-эы:

F = 27rr2. (12, VIII)

Глава IX

Одномерное и радиальное движение несжимаемой жидкости в условиях водонапорного режима

§ 1. Одномерное движение но линейному закону

фильтрации

Исследуем горизонтальный установившийся одномерный поток однородной несжимаемой жидкости в условиях водонапорного режима.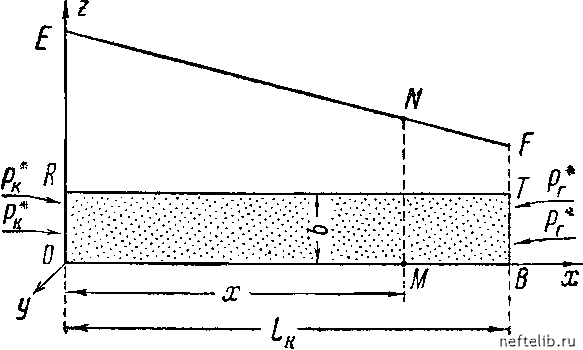

Рис. 51. Вертикальное сечение элемента пласта и пьезометрическая линия в условиях одномерного потока.

Будем считать, что движение жидкости в пористой среде подчиняется линейному закону фильтрации. Допустим, что заданы постоянные величины нриведепных давлений (а следовательно, и напоров) р* и р* в двух вертикальных сечениях OR и ВТ, перпендикулярных направлению движения потока (см. рис. 51); пусть р* > р*. На фиг. 51 изображено вертикальное сечение потока ORTB, проведенное параллельно скорости потока; плоскость этого сечения совмегцепа с плоскостью

координат XZ, а плоскость ху совмеш,ена с нижней непроницаемой границей (подогавой) пласта.

Линии OR и ВТ мы интерпретируем как сечения, соответствуюгцие контуру области питания пласта и галлерее; индексы «к» и «г» около обозначений давлений соответствуют первым буквам слов «контур» и «галлерея».

Конечно, линии OR и ТВ можно было бы интерпретировать и по-другому - как сечения, соответствуюгцие началу и концу образца горной породы (части керна) при определении его проницаемости в лабораторных условиях.

Расстояние между сечениями OR и ВТ обозначено через Lk, могцность пласта - Ь.

d В

Рис. 52. Горизонтальное сечение элемента пласта в условиях одномерного потока.

Как было выяснено в предыдугцей главе, для полного исследования потока достаточно изучить движение жидкости вдоль оси жх и ограничиться построением изобар в одной горизонтальной плоскости, например в плоскости ху. Если за опорную плоскость принять плоскость ху, то, судя по формуле (3, VIII), можно утверждать, что истинное давление в какой-либо точке опорной плоскости численно равно приведенному давлению в той же точке. Обозначим через и р постоянные заданные величины давлений на контуре области питания и в галлерее на уровне опорной плоскости; иными словами, р и р есть истинные давления в точках О и В сечения пласта на рис. 51, т. е. давления вдоль горизонтальных линий 00 и В В на рис. 52. На рис. 52 поток изображен в плане (в сечении плоскостью ху); буквой а обозначена гаирина потока. Исследование изучаемого потока сводится к определению давления, градиента давления и скорости в любой точке фильтрационного потока, к определению дебита и закона движения.