Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 [ 103 ] 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177

Подставив эти выражения в равенство (16.23), с учетом соотиошеиий (16.20) получим

vr =

.2 Л

Из равенств (16.24), (16.38) и формулы (16.20) имеем

(16.39)

(16.40) Ар

-f, то

Так как при течении по горизонтальной трубе - pF

легко видеть, что формулы (16.39) и (16.40) совпадают с полученными ранее выражениями (9.29) и (9.31). Поскольку значения а и I для капиллярного вискозиметра известны, то из формулы (16.40) следует, что для определения величины динамического коэффициента вязкости достаточно сделать одно измерение величии Ар и Q.

Для ротациоииого вискозиметра в соответствии с формулами (16.30), (16.34), (16.38) получим закон распределения скоростей в кольцевом зазоре в виде

2р J

dT =

т.. - т

2р Ажр

(16.41)

Используя формулы (16.30), (16.35), (16.38) или полагая в формуле (16.41) г = i?g, находим

J к.

Так как радиусы Д и известны, то так же, как и в случае капиллярного вискозиметра, для определения р достаточно сделать одно измерение пары значений П, М.

П. Жидкость Биигама-Шведова. Для такой жидкости в соответствии с формулой (16.16)

О, т < То,

/W=]T-Tn . (16.42)

I АМИН АРНЫЕ ТЕЧЕНИЯ НЕНЬЮТОНОВСКИХ ЖИДКОСТЕЙ

Подставив выражение (16.42) в формулу (16.23), получим

i;(r) = - f(T)dT + - f(T)dT = -

т j

Т j

Т j

0 л

Т j

f(T)dT

(16.43)

f(T)dT.

В соответствии с формулой (16.42)

при г < г,

при г > г,

г j

/(r)dr = о,

(16.44)

Г - Г,

д(-о)

(16.45)

Из формулы (16.20) следует, что

т г то го

(16.46)

где го - радиус, на котором т = то - Тогда из формул (16.43), (16.44), (16.45), (16.46) имеем

при о < г < Га,

v(r)

при го <г<а.

Таким образом, при О < г < г

i;(r) = const, то есть в потоке имеется

«ядро течения», в котором все частицы движутся с одинаковой скоростью, то есть как твердое тело (рис. 16.10).

Можно показать, что наличие ядра течения присуще любой жидкости с начальным напряжением сдвига, а не только жидкости Бингама-Шведова. Подставив соотношение (16.42) в формулу (16.24), получим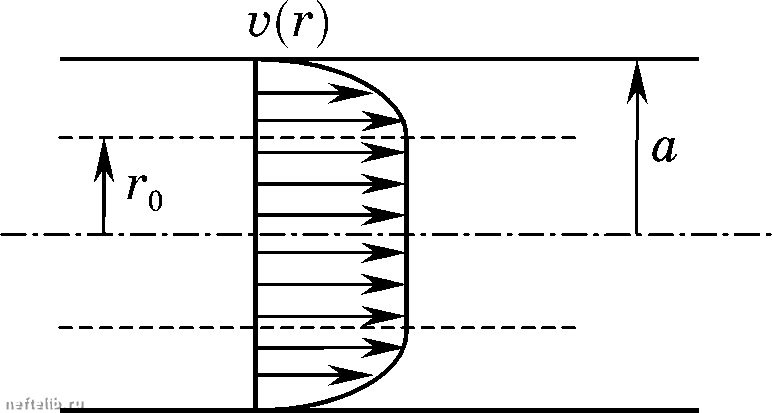

Рис. 16.10

3

т т.

4 Та 1т

3 Г. 3 т

(16.47)

или, С учетом формул (16.20) и (16.46),

S7]l

(16.48)

Выражения (16.47) и (16.48) представляют собой различную форму записи формулы Букингама. При Тд = Tq = о формула переходит в формулу Пуазейля (16.40). Из формул (16.47) и (16.48) видно, что для определения констант и Т} необходимо измерить две пары значений Ар, Q.

Рассмотрим теперь течение жидкости Бинтама-Шведова в кольцевом зазоре ротациоииого вискозиметра. Так как Д < й, то в соответствии с формулой (16.30) всегда < т. Поэтому до тех пор, пока < Tq, то есть в соответствии с формулой (16.30) М < iTtRT = Mq, сдвига ие происходит, П = о и жидкость между цилиндрами иенодвижиа. Пусть теперь > То > Tg. Так как вдоль радиуса М = const, то из формулы (16.30) следует, что

K?Tj=ro\=Kg4, где То - радиус, иа котором т = То. Тогда очевидно, что при < г < имеем т > То, а при < г < R - т < т. Следовательно, в интервале R < г < будет происходить сдвиговое течение, а при < г < R жидкость будет вести себя как твердое тело, то есть вращаться с постоянной угловой скоростью. Подставив выражение (16.42) в формулу (16.34), с учетом равеиства (16.30) получим

4in4

Го г

при Д < т- < То ,

4л77

= const при < г < Rg

в соответствии с формулой (16.30) =

2л-т„

, то есть с ростом М ве-

личина То и, следовательно, область, охвачеииая сдвиговым течением, возрастают. При То > Tg сдвиговым течеьшем охвачен весь интервал < г < i?g, и в соответствии с формулами (16.30) и (16.35) угловая скорость вращения виешиего цилиндра равна

П = -2 J

Т- То (/Т

(16.49)