Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 [ 85 ] 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177

Обратимся к иостроеиию решения задачи Блазиуса. Уравиеиия (14.16) и граничные условия (14.17) содержат систему определяющих параметров

из которых только два обладают независимыми размерностями. Следовательно, из этой системы можно составить две безразмерных комбинации, иаиример,

Тогда искомые функции и{х,у), v{x,y) можно представить через безразмерные функции / и Ф как

u = U,f

(14.18)

Сделаем в уравнениях (14.16) и граничных условиях (14.17) замену переменных

X = 1х, у =

и = ищ, V =

vU, I

(14.19)

где I - некоторый линейный размер.

Подставив соотношения (14.19) в уравиеиия (14.16) и граничные условия (14.17), получим

дх, ду, ду1

dx, ду,

u,=v,=Q> при i/i = О, и,=\ при у,

(14.20) (14.21) (14.22)

Из формул (14.19) следует, что

У У1

= л -1 = vx \Х JX,

vUr.

= v,\- = V,JX.

и равеиства (14.18) могут быть представлены в виде

f У1 У1

V й Ух

0 л/ "1

в то же время уравиеиия (14.20), (14.21) и граничные условия (14.22) ие содержат в себе длины I. Следовательно, решение этих уравнений ие

может зависеть от , то есть от аргумента

, поэтому

г л

г л

V, =

(14.23)

Из уравиеиия иеразрывиости (14.21) следует, что существует функция тока y/{xi, г/J, так что

ду/ ду1

Д = -

ду/ дх

Положим

Г л

(14.24)

Тогда

W = У, = -

2JI, ddx,

(14.25)

Подставив соотиошеиия (14.24) и (14.25) в уравиеиие (14.20), получим ,d£dl J j, d£dl dJ d£dl\dl

d dx 2 d Эг/i d у d dy) dy

или, после дифференцирования и приведения подобных членов,

2- = 0.

(14.26)

Из граничных условий (14.22) и формул (14.24), (14.25) следует, что граничные условия для уравиеиия (14.26) имеют вид

(0) = 0, (0) = 0, Н = 1. (14.27)

Таким образом, уравиеиия в частных производных (14.16) с граиич-иыми условиями (14.17) свелись к обыкновенному нелинейному дифференциальному уравнению (14.26) с краевыми условиями (14.27). Решение этой задачи может быть построено числеиио с высокой точностью, что и было сделано давно.

ГЛАВА XIV

Из формул (14Л9), (14.23), (14.24) и (14.25) следует, что

о

.(14.28)

Графики распределения продольной и поперечной составляющих скорости в пограничном слое представлены на рис. 14.3 и 14.4, соответственно.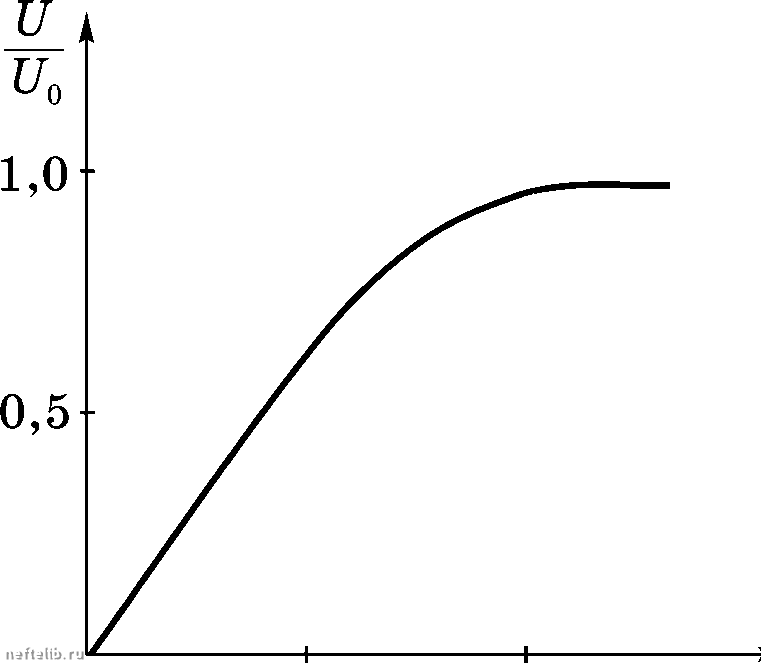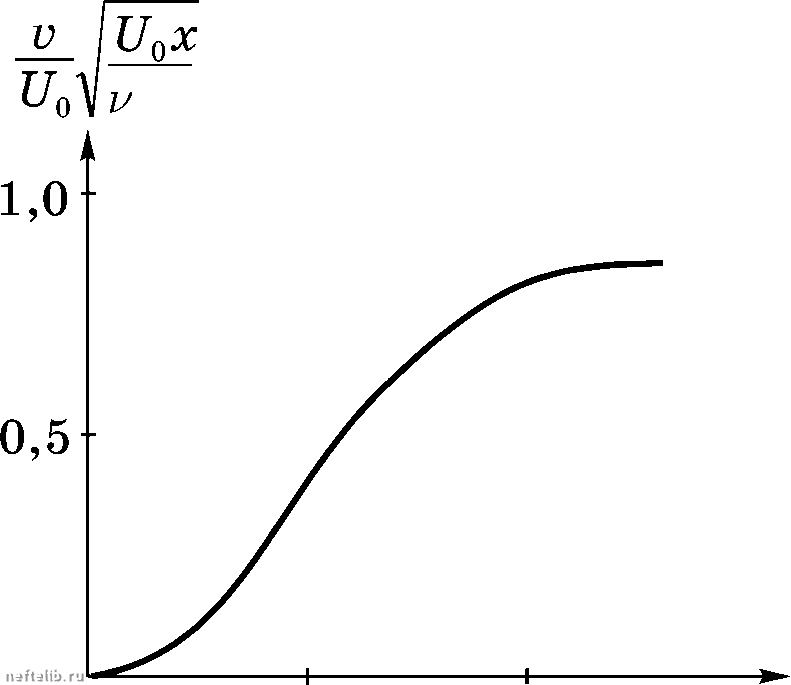

Рис. 14.3

Рис. 14.4

Принимая, что на внешней границе пограничного слоя

первой формулы (14.28) имеем

0,99 = ф

Тогда из таблицы функции 9\) следует, что

у 5 -5

0,99 из

Подставляя это значение во вторую формулу (14.28) и используя таблицы функций к), (), получим на внешней границе погранично-

го слоя

5(5)-(5)] - 0,837