Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 [ 120 ] 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177

основные определения и понятия фильтрации

обладать даже ньютоновские жидкости. Но с ростом скорости этот эффект в ньютоновских жидкостях быстро исчезает.

В нефтегазовом деле к жидкостям, проявляющим неньютоновские свойства, относятся так называемые аномальные нефти и буровые растворы.

Классическим примером выражения закона фильтрации для неньютоновской жидкости является закон фильтрации с предельным (начальным) градиентом. Этот закон фильтрации выписывается для вязкопластичной жидкости Бингама-Шведова и имеет вид

grad р

при grad р > у,

(18.26)

О при grad р < у

Как следует из соотношепий (18.26), фильтрационпое течение возможно лишь при градиентах давления, превышающих некоторое значение 7, которое называется на-

чальным (предельным) градиентом. При меньших значениях градиента давления фильтрационное течение отсутствует. Величина начального

градиента зависит от начального напряжения сдвига жидкости Tq и эффективного диаметра капилляра d.

На рисунке 18.9 приведены графики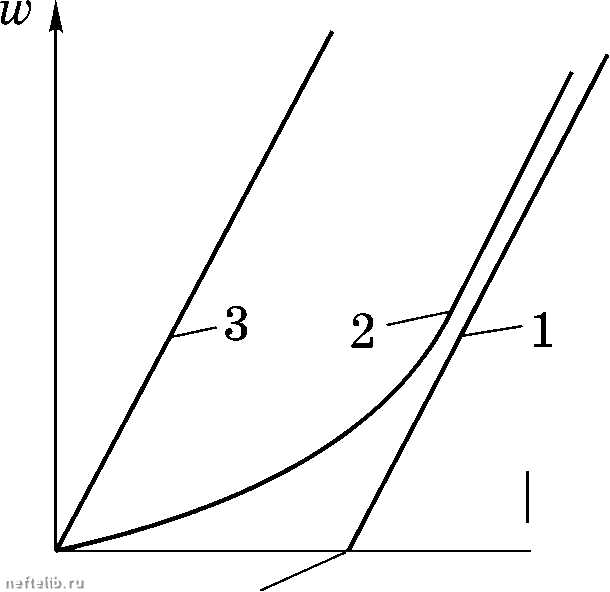

grad р

7= grad7

Рис. 18.9. Графики зависимости W от

grad р

зависимости скорости фильтрации j вязкопластической жидкости от градиента фильтрационного дав-

ления, соответствующие линейным

с предельным градиентом; 2 - для реальных неньютоновских неф-

и нелинейным законам фильтрации.

теи:

3 - для закона Дарси.

§7. Структурные модели пористых сред

Как уже отмечалось выше, реальные коллекторы углеводородного сырья имеют сложное строение пустотного пространства, которое образуется норовыми каналами с резко изменяющимися диаметрами и нанравле-ниями, состоят из частиц различной формы и размеров и т.д. Поэтому по-

строепие аналитических решении, учитывающих все перечисленные осо-бенпости реальных пористых сред, практически, невозможно. В связи

с этим в подземной гидромеханике часто пользуются упрощенными идеа-

ГЛАВА XVIII

лизированными моделями пористой среды. К таким моделям относятся идеальные (капиллярные) и фиктивные (корпускулярные) грунты (среды). В корпускулярных моделях пористая среда моделируются шарами, а в капиллярных - капиллярными трубками.

Простейшая корпускулярная модель, в которой пористая среда моде-

лируется упаковкой шаров постоянного диаметра, называется фиктивным грунтом (или фиктивной пористой средой). Простейшая капиллярная модель, в которой пористая среда моделируется капиллярными трубками постоянного диаметра, уложенными с постоянным периодом, называется идеальным грунтом (или идеальной пористой средой). Наиболее популяр-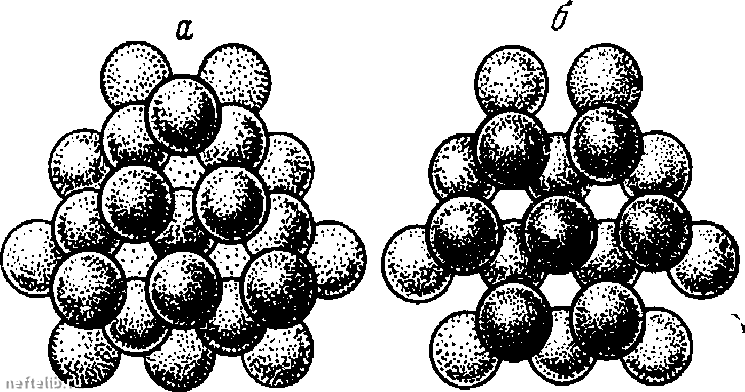

Рис. 18.10. Слой шаров, плотнейшим Рис. I8.II. Проекции двух основных образом прилегающих друг к другу плотнейших упаковок шаров:

а - кубическая, б - гексагональная

ные модели фиктивного грунта соответствуют наиболее плотным упаковкам шаров. Две основные упаковки - кубическая и гексагональная получаются следующим образом: первый плоский слой уложен так, что каждый

шар касается шести соседних, каждый шар второго слоя помещается в уг-тубление между тремя шарами первого слоя (рис. 18.10, 18.11). При нало-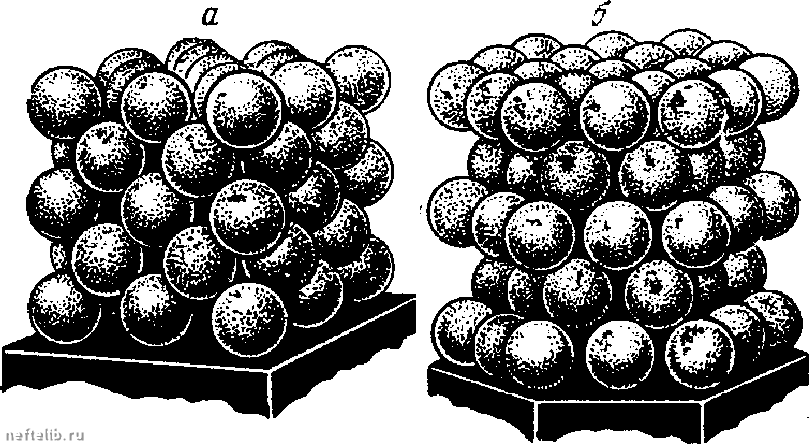

жении третьего слоя возможны два варианта. В первом варианте (кубическая упаковка) каждый шар третьего слоя лежит на трех шарах второго слоя таким образом, что под шаром третьего слоя нет шара первого слоя (рис. 18.12). Во втором варианте (гексагональная упаковка)

Рис. 18.12. Плотнейшие упаковки шаров по кубической (а) и гексагональной (б) схемам

каждый шар третьего слоя лежит на трех шарах второго, но под каждым шаром третьего слоя оказывается шар первого слоя. Кроме указанной

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ПОНЯТИЯ ФИЛЬТРАЦИИ

наиболее плотной упаковки с кубической симметрией рассматривают и та-

кую упаковку, когда в первом слое каждый шар касается только четырех шаров, а все последующие слои повторяют первый. Назовем последнюю кубическую упаковку шаров рыхлой кубической упаковкой.

Для капиллярных моделей идеального грунта наиболее простые модели получаются при взаимно перпендикулярном расположении капилляров.

Введепие в рассмотрение идеальных и фиктивных грунтов и получаемое в результате упрощение структуры норового пространства позволяют находить аналитические формулы, связывающие между собой фильтрационно-емкостные характеристики таких упрощенных пористых сред, и далее обобщать получепные соотпошения на реальные пористые среды. Рассмотрим в начале основные соотношения для фиктивного грунта.

Для фиктивного грунта достаточно просто получается соотношепие, связывающее удельную поверхность с пористостью упаковки т и диаметром шаров D. Возьмем объем, в котором имеется п шаров. Тогда весь объем можно представить как сумму объема пустот и шаров -

Отсюда для т получаем

т - \

(18.27)

Удельная поверхность, очевидно, равна площади поверхности одного

шара умноженной на число шаров в упаковке

(18.28)

Из соотношений (18.27) и (18.28) следу-

ет, что

6(1 - т) D

(18.29)

Более детальное исследование модели фиктивного грунта было предпринято С. С лихтером, который схематизировал наиболее плот-

ные упаковки шаров, введя элементарную ячейку упаковок шаров (рис. 18.13) и нашел следующие аналитические формулы для пористости и просветпости:

т = 1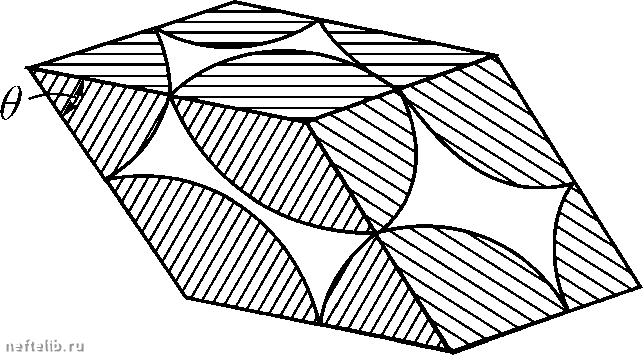

Рис 18.13. Элементарная

ячейка упаковки шаров

6(1 - COS 1 + 2 COS 6>

(18.30)