Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 [ 161 ] 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177

496 ГЛАВА XXIV

Приняв во внимание, что р{х, t) = [t] нрн х = О, из (24.1) найдем

откуда

ОМ = Р (24.5.)

2kBh 2

Подставив равеиства (24.3)-(24.5) в соотиошеиие (24.2), получим

2kBh

или, так как Q = const.

2Q = qUi

k dt

откуда следует

2Kdt = dl [к = к1[0*)).

Проинтегрируем получеиное соотиошеиие и найдем

l{t)=42Kt. (24.6)

Следовательно, формула для расиределення давления в пласте (24.1) будет иметь вид

kBh (24.7)

p{x,t) = , X > 42М.

Значения денрессни р - р но ирнближенной формуле (24.7) значительно отличаются от данных расчета но точной формуле (24.39): погрешность составляет 25%.

Случай 2. Приток к галерее, иа которой поддерживается постоянное забойное давление р = const. В таком же пласте, как н в случае 1, в момент времени t = О пущена эксплуатацнонная галерея с постоянным забойным давлением р = const. До пуска галереи давление во всем пласте бьшо одинаковым н равным р. Требуется иайти расггоеделенне давления, закон ие-ремещения границы возмущенной области l[t) и изменение дебита галереи во времени Q{t).

Дебит галереи в условиях установившегося движения, очевидно, можно выразить следующим образом:

р lit] р Эх

Задача решается аналогично предыдущему случаю с той лишь разницей, что в уравненне для упругого запаса жидкости (24.2) нужно подставить выражения

V{t) = Bhl{tl

Ар = л - Р = л - " = " ,

pl(t)

Таким образом, в результате получим

Кр. - Рг)

pi{t)

Bhdt = р d

Проведя арифметические преобразования в этом соотношении, и выполнив иитегрироваиие, найдем закон движеиия границы возмущенной области

l{t) = 2[fCt .

Следовательно, распределение давления в возмущенной зоне пласта определяется соотношением

p{x,t)= р-{р-р} 1--7= , 0<x<2vst,

I. 2Vst j (24.8)

p{x,t)= р, X > 2Vst,

a дебит галереи - соотношением

Q{t)=iPBh. (24.9)

2vst

Погрешность расчета дебита галереи по приближенной формуле (24.8) по сравиеиию с расчетами по точной формуле (23.27) составляет 11%. Следовательно, методом последовательной смены стационарных состояний лучше пользоваться в случае неустановившихся ирямолниейно-иараллель-иых потоков прн заданной постоянной депресснн.

Плоскорадиальныи неустановнвшнйся фильтрационный поток упругой жидкости.

Случай 1. Приток к скважине, на которой поддерживается постоянный дебнт Q. Пусть в неограниченном горизонтальном пласте постоянной толщины h в момент времени t = О пущена добывающая скважина радиусом с постоянным дебитом Q. До иуска скважииы давление во всем пласте было одинаковым н равным р.

В соответствии с методом ПССС принимаем, что через время t после пуска скважииы вокруг нее образуется возмущенная область радиусом R{t),

ГЛАВА XXIV

в которой давление будет распределено по стационарному закону

Р(г, t)

iTtkh

(24 Л 0)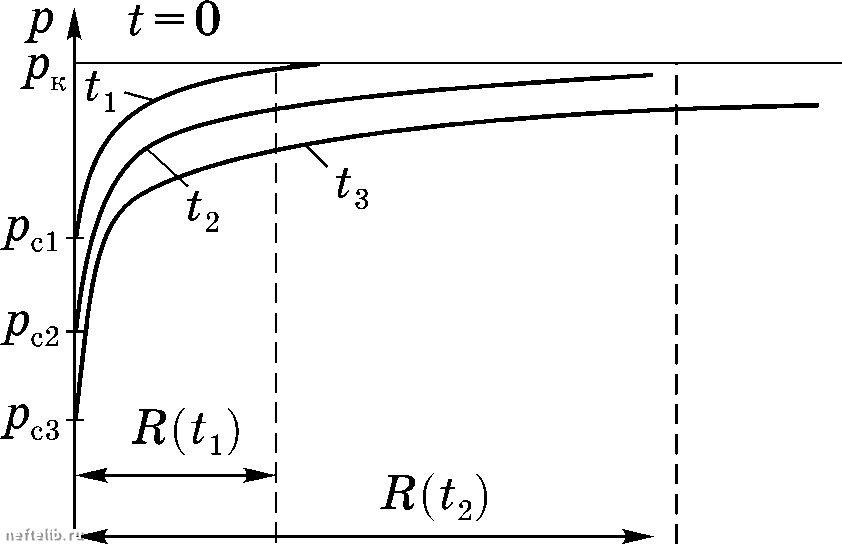

В остальной части пласта со-

у /у

храняется начальное пластовое давление р.

Требуется найти закон движения границы возмущенной области R{t).

Кривые распределения давления в разные моменты времени в таком потоке приведены на рис. 24.2. Дебит скважины, очевидно, будет

/77777777777777777777777777777777777

описываться формулой, аналогичной формуле Дюпюи,

Рис. 24.2. Кривые распределения давления в плоскорадиальном потоке в разные моменты времени по методу ПССС (отбор осуществляется при условии Q = const)

2М(р,-рМ

(24Л1)

Размеры возмущенной области

найдем из уравнения материального баланса (24.2) при

V{t) = 4R(t)-r}h,

Р = Рк-Р

(24 л 2)

Средневзвешенное пластовое давление р в установившемся плоскорадиальном потоке (см. гл. XX, §3)определяется по формуле (20.25)

Р = Р

Рк-Р

2ln(R(t)/rS

откуда, учитывая (24.11), находим

Р Рк-Р

Рк-Р

2ln{R(t)/rJ 4М

(24.13)

Закон движения границы возмущенной области R{t) найдем, подставив выражения (24.12) и (24.13) в уравнение материального баланса (24.2),

4fcdt = d(R(t)-r

откуда после интегрирования в пределах от О до и от до R{t) найдем

R(t)

(24.14)