Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 [ 50 ] 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177

ПЛОСКОПАРАЛЛЕЛЬНЫЕ ТЕЧЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ

Формула (8.23) дает связь между скоростями потока в плоскостях z и . Так как, по условию, F\z) О и F\z) Ф , то из этого следует,

что при конформном преобразовании критические точки переходят в критические точки и никаких новых критических точек возникнуть не может.

Зависимость W = W{z) можно рассматривать как отображение области D в плоскости Z на область Z) в плоскости W (рис. 8.11). Так как

dW dW

функция W\z) аналитическая, то всюду, где -;- Ф О м -;- Ф это

отображение будет конформным. В плоскости W линии тока у/ = const суть прямые, параллельные оси Оср, а эквипотенциали (р = const -

- прямые, параллельные оси Оу/. Следовательно, W = W{z) представляет собой отображение потока в плоскости z на прямолинейное поступательное движение в плоскости W.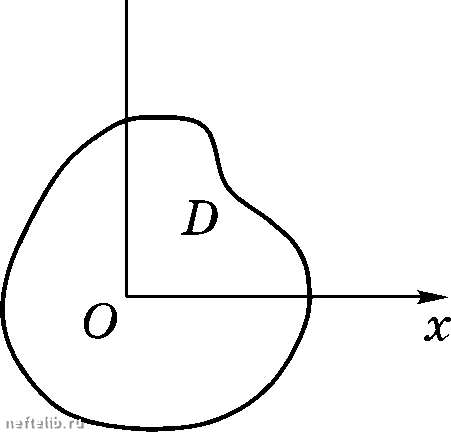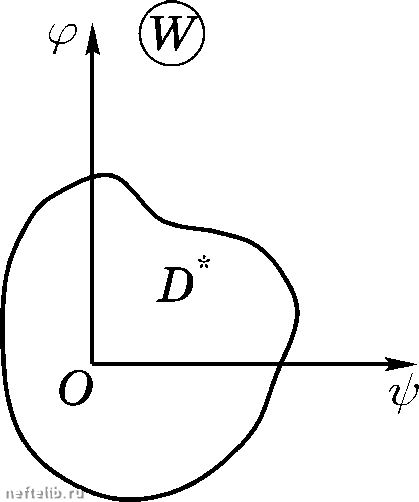

Рис. 8.11

Пусть в плоскости Z имеется линия тока у/ = const с угловыми точ- У

ками и В (рис. 8.12) и пусть W{z) - комплексный потенциал этого течения. В плоскости W все ли-

НИИ тока переидут в прямые линии, то есть в точках АиВ конформность нарушается.

В примере 3 настоящего параграфа было показано, что комплекс-

ный потенциал вида

W-W, = (z-zJ

Рис. 8.12

(8.24)

§4. Преобразование Жуковского

Рассмотрим комплексный нотеициал

f d2 Л

W = h

= (р + iy/, (8.25)

описывающий симметричное обтекание цилиндра радиуса Я (рис. 8.13). Область течения - вся плоскость г, внешняя но отношению к цилиндру. Найдем соответствующую ей область в плоскости W".

Линии тока у/ = const в плоскости W суть прямые. Из формулы (8.25) имеем

(р = k

г + -

cos в, у/ = k

sin в

Линии тока = О в плоскости z соответствуют окружность радиуса R с центром в начале координат и нолусегмеиты [R < д: < <») и (- < д: < -Я].

Точкам А и В с координатами = z = Я (рис. 8.13) в плоскости W" соответствуют точки А, иа оси у/ = О с координатами

= -2кЯ, (р = 2кЯ. Для точки С с координатами z = Re иа плоскости W имеем

у/ = О, (р = 2кЯ cos в,

то есть точка С отображается иа плоскости W во виутреииость сегмента [-2кЯ, 2кЯ\.

Итак, функция (8.25) представляет собой отображение плоскости z иа плоскость W", при котором внешность цилиндра отображается иа внешность отрезка АД, а обтекание цилиндра преобразуется в обтекание отрезка Д Д.

описывает обтекание угла а = - с вершиной в точке z = z. В точке А

а < ж, 7г>1,ав точке В а > ж, п < \. Тогда из формулы (8.24) следует,

dW dW

что -= о нрн г = , -= нрн г = , то есть нрн обтекании

dz dz

вдающегося угла у = О, а нрн обтекании острия у = .

Из интеграла Коши-Лаграижа вытекает, что нрн у = р = -<» и,

следовательно, нотенциальное обтекание острия физически невозможно.

ПЛОСКОПАРАЛЛЕЛЬНЫЕ ТЕЧЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ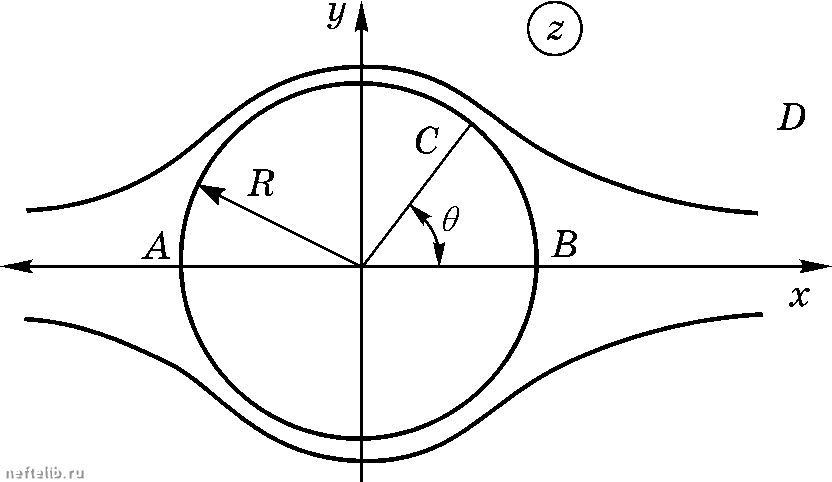

а в,

Рис. 8.13

При Z = +R производная

обращается в нуль, то есть в точках АиВ конформность отображения нарушается. Бесконечно удаленная точка плоскости z переходит в бесконечно удаленную точку плоскости W. Направление скорости в бесконеч-

= k, а k > О - действительное число.

ности сохраняется, так как

Преобразование вида (8.25) называется преобразованием Жуковского . Возьмем в плоскости z окружность с центом в начале координат и ра-

диусом г > R. Тогда z = ге ив соответствии с формулой (8.25)

(р = k

COS в, у/ = k

sin (9,

(8.26)

то есть преобразование Жуковского отображает внешность окружности в плоскости Z на внешность эллипса в плоскости W, причем точки

и суть фокусы этого эллипса.

Можно показать, что окружности с центром в точке (х, О) соответствует в плоскости W симметричный крылообразный профиль С - руль Жуковского, окружности с центром в точке [О, - дуга окружности, окружности с центром в точке (х, г/) - несимметричный крылообразный

профиль G - профиль Жуковского (рис. 8.14). Угол у задней кромки профилей Жуковского равен 2л", что и является их отличительной особенностью.

Николай Егорович Жуковский (1847-1921), один из основоположников современной аэромеханики. Формулы (8.26) представляют собой параметрические уравнения эллипса с полуосями

k\r +

Ъ = k\r

И фокусами В точках (р = ±2kR.